Analyse der Pfadflächen
Da es aber trotz der "intelligenten" Pfadsuche noch übermäßig viele Möglichkeiten für den gültigen Pfad gibt, müssen weitere Optimierungen vorgenommen werden.
Jeder Pfad spannt eine Fläche auf, deren Abmessungen sich aus den Schritten nach rechts und nach unten ergeben.
Wichtig ist dabei der erste Schritt:
- Geht der erste Schritt im Pfad nach rechts ergibt sich die Fläche zu:
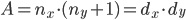
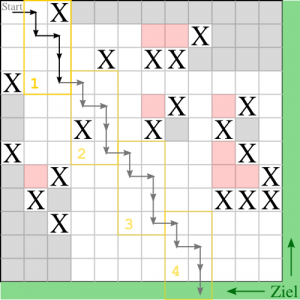
Der im Bild dargestellte Pfad lautet:
RDRDD und hat die Länge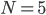 
.
Die Anzahl an Schritten nach rechts ist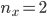 
und 
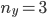nach unten.
Er spannt ein Rechteck mit den Seitenlängen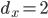 
und 
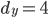auf.
- Geht der erste Schritt im Pfad nach unten ergibt sich die Fläche zu:
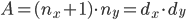
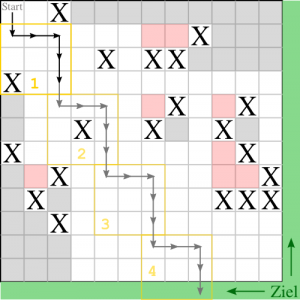
Der im Bild dargestellte Pfad lautet:
DRRDD und hat die Länge .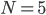
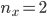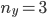Die Anzahl an Schritten nach rechts ist und nach unten.
Er spannt ein Rechteck mit den Seitenlängen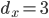 
und 
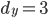auf.
Beim Überprüfen, ob ein Pfad zum Ziel führt, kann es sein, dass man z.B. erst beim dritten Durchlaufen des Pfades auf ein Hindernis stößt. Um den Vorgang der Überprüfung zu beschleunigen, kann man nachfolgendes Verfahren verwenden, um das Hindernis schon beim ersten Durchlaufen des Pfades zu erkennen.
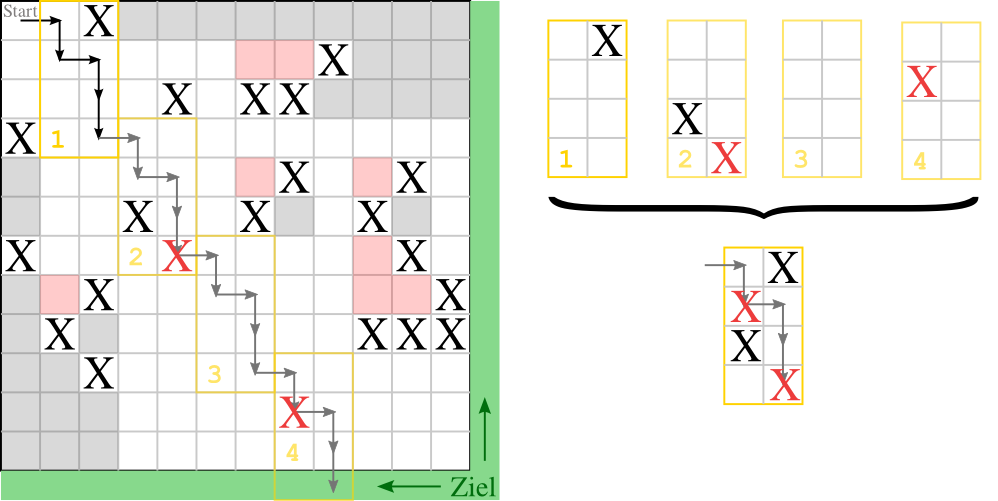
Dabei soll folgendes Spielfeld als Beispiel dienen:
- Es werden alle Flächen, die von einem Pfad durchlaufen werden, übereinander gelegt (natürlich stellen auch Sackgassen und unerreichbare Felder ein Hindernis dar).
- Beim erstmaligen Durchlaufen der "komprimierten" Fläche kann nun das Hindernis aus Fläche "4" schon nach dem zweiten Schritt erkannt werden.
Allgemein gilt:
Betrachtet man alle möglichen Anzahlen von Schritten nach rechts bzw. unten für einen Pfad der Länge N, können folgende Flächen existieren:
"Alle nach unten", "Ein Schritt nach rechts, der Rest nach unten", "Zwei nach Rechts, der Rest nach unten", ... , "Alle außer einem Schritt gehen nach rechts", "Alle nach rechts".
In Kurzschreibweise: [dx * dy]
[1 * N], [2 * (N-1)], [3 * (N-2)], …, [N * 1], also insgesamt N verschiedene Flächen.
Diese Flächen müssen zusätzlich noch jeweils anhand der Richtung des ersten Schrittes (nach rechts oder nach unten) unterschieden werden (siehe oben) ? Es gibt also 2 * N Flächen.
Es ergibt sich also eine weitere Optimierungsmöglichkeit:
Berechnet man im Vornherein alle möglichen "komprimierten" Pfadflächen, so kann man beim Durchprobieren des Pfades sehr schnell auf die für den Pfad zutreffende "komprimierte" Pfadfläche zugreifen und muss diese nicht jedes Mal neu erstellen. Es handelt sich also um eine Aufgabe, die für jede Pfadlänge N einmal ausgeführt werden muss.
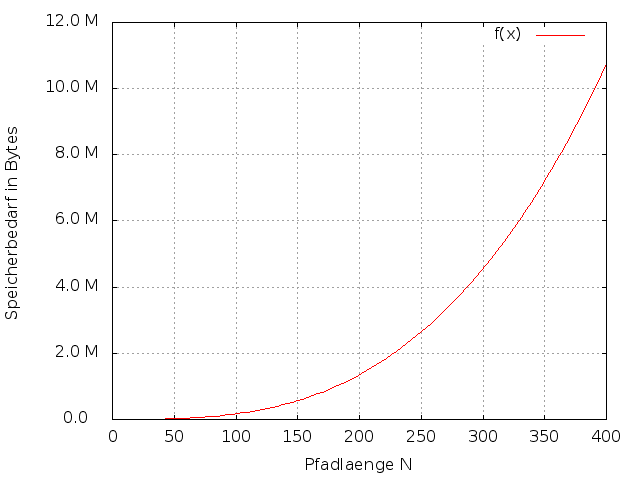
Der Speicherplatzbedarf für die im Voraus berechneten "komprimierten" Pfadflächen für einen Pfad der Länge N, kann - unter der Annahme, dass eine Pfadfläche die Anzahl ihrer Felder in Bytes an Speicherplatz belegt - mit folgender Summenformel berechnet werden:
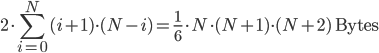
Betrachtet man den benötigten Speicherplatz über die Pfadlänge N,
wird ersichtlich, dass dieses Verfahren sich mit heutigen Arbeitsspeichergrößen und der hier maximalen Pfadlänge von 361 gut umsetzen lässt.
Fazit
Mit allen oben gezeigten Optimierungen kann ich mit meiner Implementierung in Python z.B. Level 500 in durchschnittlich 17,5 Sekunden lösen.
